


Next: Using only image data
Up: Crash course in optical
Previous: Basic problem.
Let 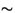 represent the n observed images,
and let
represent the n observed images,
and let 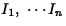 represent a word hypothesis,
that is, a particular sequence of n letters whose likelihood
of having generated the observed images is to be evaluated.
Then using Bayes' theorem one may express the conditional
probability that the given word hypothesis is correct given
the observed images as follows:
represent a word hypothesis,
that is, a particular sequence of n letters whose likelihood
of having generated the observed images is to be evaluated.
Then using Bayes' theorem one may express the conditional
probability that the given word hypothesis is correct given
the observed images as follows:
| 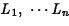 |
(1) |
Here, C is a normalization constant (this just means that you
want to make sure that all the probabilities add up to 1).
The basic problem thus becomes a concrete optimization problem:
maximize the right-hand side of the above equation over
all possible word hypotheses 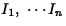 .
The solution to this problem depends on the model that one
assumes for image generation and letter co-occurrence as
encoded in the two terms on the right-hand side above.
Some comments on this statement follow.
.
The solution to this problem depends on the model that one
assumes for image generation and letter co-occurrence as
encoded in the two terms on the right-hand side above.
Some comments on this statement follow.
Sergio A. Alvarez
4/26/2000
![]() represent the n observed images,
and let
represent the n observed images,
and let ![]() represent a word hypothesis,
that is, a particular sequence of n letters whose likelihood
of having generated the observed images is to be evaluated.
Then using Bayes' theorem one may express the conditional
probability that the given word hypothesis is correct given
the observed images as follows:
represent a word hypothesis,
that is, a particular sequence of n letters whose likelihood
of having generated the observed images is to be evaluated.
Then using Bayes' theorem one may express the conditional
probability that the given word hypothesis is correct given
the observed images as follows: