


Next: Formulation as a graph
Up: Crash course in optical
Previous: Using only image data
A slightly better model uses transition probabilities to represent
letter-order restrictions. For each pair (x,y) of letters, a number
P(y|x) between and 1 is given, corresponding to the fraction
of words in which letter y is observed to follow immediately after
letter x. We assume that the prior probabilities of all letters
are also known; these are numbers between and 1 that measure the
relative frequencies of the letters in the given language (English,
for example). These probabilities allow one to assess the likelihood
of a given sequence of letters in the absence of image data.
The likelihood of observing the sequence 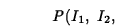 can
be computed as a product:
can
be computed as a product:
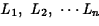
The language generation model encoded in the transition probabilities
can now be combined with the image generation model implicit in the
conditional probabilities P(Ik | Lk) as described previously to
quantify the likelihood of a given sequence of letters in the presence
of specific image data.
Indeed, Eq. ![[*]](/Graphics/LaTeX/icons.gif/cross_ref_motif.gif) becomes:
becomes:
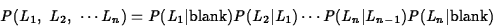
The text recognition problem therefore reduces to the following
optimization problem: maximize the likelihood that appears on
the right-hand side of the above equation over all letter sequences
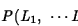 .
The winning letter sequence is the one most likely to have led to
the observed images, given the known transition probabilities
between letters.
.
The winning letter sequence is the one most likely to have led to
the observed images, given the known transition probabilities
between letters.



Next: Formulation as a graph
Up: Crash course in optical
Previous: Using only image data
Sergio A. Alvarez
4/26/2000
![]() can
be computed as a product:
can
be computed as a product:
![]()
![]()